Už na gymnáziu mě zaujal jeden příběh, který mi přiblížil vzoreček aritmetické posloupnosti . Víte, proč vzorec vypadá tak, jak vypadá? Co jednotlivé symboly znamenají a jak malý kluk dokázal zpaměti sečíst čísla od 1 do 100? Čtěte dále a dozvíte se to i Vy. Uvidíte, že si tento příběh zapamatujete a až přijde čas, vybaví se Vám třeba u státní maturity nebo na zkoušce.

Devítiletý mladý chlapec, Johann Carl Friedrich Gauss , se narodil v Brunšviku v Německu. Proslavil jako významný matematik a fyzik. Po něm známe například součet aritmetické posloupnosti, ale i Gaussovo rozdělení pravděpodobnosti (o tom někdy později :)). Tento matematik toho má na kontě opravdu mnoho a o jeho genialitě se mluvilo už od dětství. Nejznámější je ovšem jeho příběh, který se mu stal v devíti letech.
Jednoho dne ve škole zadal žákům, ať sečtou všechny číslice od 1 do 100. Žáci začali počítat, ale za chvilku se ozval malý Gauss a odpověděl učitelovi, že už výsledek zná. Vypočítal ho snadno a zpaměti. Učitel se velmi podivil, že je tak rychlý, a zeptal se ho, jak na výsledek přišel. On avšak řekl, že si napsal číslice seřazeně za sebou. Všiml si, že vždy dané hodnoty z kraje (tj. první a poslední číslici, druhou a předposlední, atd.), když sečte, dostane vždy součet 101 ( 1+100, 2+99, 3+98, ... ). Takových dvojic vytvořil 50 (což je přesná půlka ze 100). Takže potom ciferný součet spočítal vynásobením 101 a 50. Výsledek je tedy 5050!
Když se na to podíváme, vidíme, že to dává opravdový smysl. Takže vzoreček pro součet aritmetické posloupnosti vypadá takto:
S_n = \frac{n}{2} * (a_1 + a_n)
přičemž
- S_n je součet n prvků (nějakého počtu číslic, 100, 10, 15000),
- n je počet prvků (číslic),
- a_1 je první člen aritmetické posloupnosti (první číslice)
- a_n je poslední člen aritmetické posloupnosti (poslední číslice).
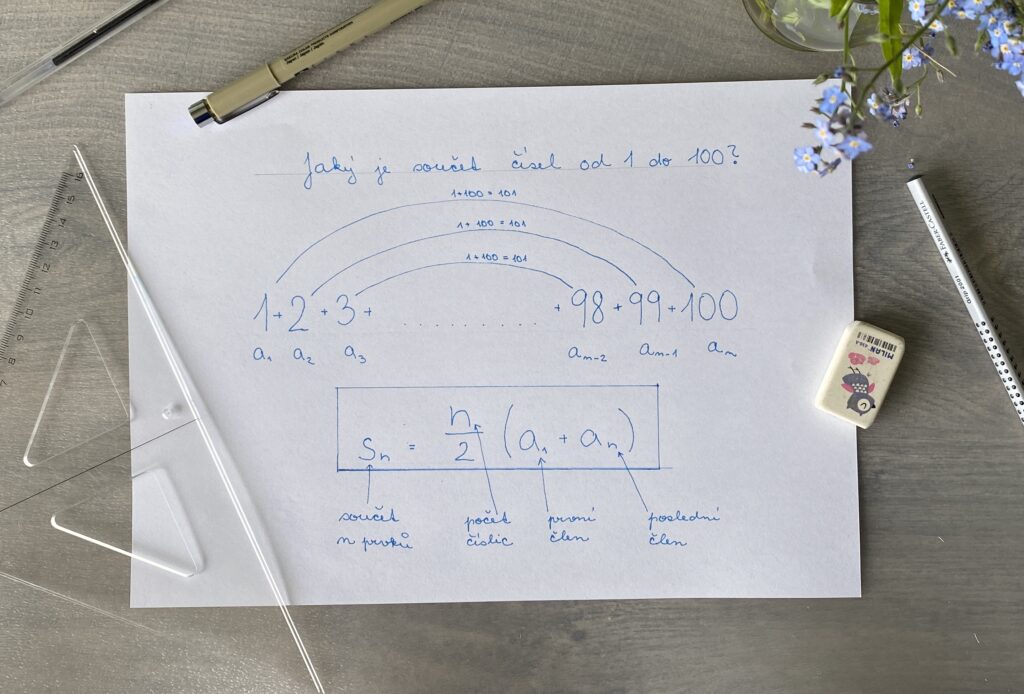
Vzoreček tedy znamená, že sečtu první a poslední číslice z dané posloupnosti (členy posloupnosti) a tím vynásobím polovinou z celkového počtu číslic. Získám tedy počet dvojic, které vynásobím součtem první a poslední číslice. A mám tak celkový součet všech cifer!
Tak co, myslíte si, že si tento příběh zapamatujete a chápete, co vzorec pro součet několika prvků znamená? Možná si myslíte, že tento příklad nikdy nevyužijete, ale uvidíte sami.
Pokud máte jakékoliv otázky k tomuto tématu, napište je pod tento příspěvek a ráda Vám je zodpovím. Již brzy se můžete těšit na pokračování.

